Skip to contents

So you're trying to choose an event-study estimator...

event_study.Rmd

The command event_study presents a common syntax that estimates the event-study TWFE model for treatment-effect heterogeneity robust estimators recommended by the literature and returns all the estimates in a data.frame for easy plotting by the command plot_event_study. The general syntax is

event_study(
    data, yname, idname, tname, gname, 
    estimator,
    xformla = NULL, horizon = NULL, weights = NULL
)

The option data specifies the data set that contains the variables for the analysis. The four other required options are all names of variables: yname corresponds with the outcome variable of interest; idname is the variable corresponding to the (unique) unit identifier, \(i\); tname is the variable corresponding to the time-period, \(t\); and gname is a variable indicating the period when treatment first starts (group-status).

Event Study Estimators
Estimator R package and Estimator Option Type Comparison group Main Assumptions Uniform inference of estimates

Gardner (2021)

did2s

 Imputes \(Y(0)\) Not-yet- and/or Never-treated
  • Parallel Trends for all units
  • Limited anticipation*
  • Correct specification of \(Y(0)\)

Borusyak, Jaravel, and Spiess (2021)

{didimputation}

 Imputes \(Y(0)\) Not-yet- and/or Never-treated
  • Parallel Trends for all units
  • Limited anticipation*
  • Correct specification of \(Y(0)\)

Callaway and Sant'Anna (2021)

did

 2x2 Aggregation Either Not-yet- or Never-treated
  • Parallel Trends for Not-yet-treated or Never-treated
  • Limited anticipation*
✔

Sun and Abraham (2020)

{fixest/sunab}

 2x2 Aggregation Not-yet- and/or Never-treated
  • Parallel Trends for all units
  • Limited anticipation*

Roth and Sant'Anna (2021)

{staggered}

 2x2 Aggregation Not-yet-treated
  • Treatment timing is random
  • Limited anticipation*
* Anticipation can be accounted for by adjusting 'initial treatment day' back \(x\) periods, where \(x\) is the number of periods before treatment that anticipation can occur.

There are five main estimators available and the choice is specified for the estimator argument and are described in the table above.1 The following paragraphs will aim to highlight the differences and commonalities between estimators. These estimators fall into two broad categories of estimators. First, did2s and {didimputation} are imputation-based estimators as described above. Both rely on “residualizing” the outcome variable \(\tilde{Y} = Y_{it} - \hat{\mu}_g - \hat{\eta}_t\) and then averaging those \(\tilde{Y}\) to estimate the event-study average treatment effect \(\tau^k\). These two estimators return identical point estimates, but differ in their asymptotic regime and hence their standard errors.

The second type of estimator, which we label 2x2 aggregation, takes a different approach for estimating event-study average treatment effects. The packages did, fixest and {staggered} first estimate \(\tau_{gt}\) for all group-time pairs. To estimate a particular \(\tau_{gt}\), they use a two-period (periods \(t\) and \(g-1\)) and two-group (group \(g\) and a “control group”) difference-in-differences estimator, known as a 2x2 difference-in-differences. The particular “control group” they use will differ based on estimator and is discussed in the next paragraph. Then, the estimator manually aggregate \(\tau_{gt}\) across all groups that were treated for (at least) \(k\) periods to estimate the event-study average treatment effect \(\tau^k\).

These estimators do not all rely on the same underlying assumptions, so the rest of the table tries to concisely summarize the differences between estimators. The comparison group column describes which units are utilized as comparison groups in the estimator and hence will determine which units need to satisfy a parallel trends assumption. For example, in some circumstances, treated units will look very different from never-treated units. In this case, parallel trends may only hold between ever-treated units and hence only these units should be used in estimation. In other cases, for example if treatment is assigned randomly, then it’s reasonable to assume that both not-yet- and never-treated units would all satisfy parallel trends.

For estimators labeled “Not-yet- and/or never-treated”, the default is to use both not-yet- and never-treated units in the estimator. However, if all never-treated units are dropped from the data set before using the estimator, then these estimators will use only not-yet-treated groups as the comparison group. did provides an option to use either the not-yet- treated or the never- treated group as a comparison group depending on which group a researcher thinks will make a better comparison group. {staggered} will automatically drop units that are never treated from the sample and hence only use not-yet-treated groups as a comparison group.

The next column, Main Assumptions, tries to summarize concisely the main theoretical assumptions underlying each estimator. First, the assumptions about parallel trends match the previous discussion on the correct comparison group. The only estimator that doesn’t rely on a parallel trends assumption is {staggered}, instead relying on the assumption that when a unit receives treatment is random.

The next assumption, that is common across all estimators, is that there should be “limited anticipation” of treatment. In general, anticipatory effects are when units respond to treatment before it is actually implemented. For example, this can be common if the news of a treatment triggers behavior responses before the treatment is put in place. “Limited anticipation” is when these anticipatory effects can only exist in a “few” pre-periods.2 In any of these cases, “treatment” should be manually moved back by the maximum number of periods where anticipation can occur. For example, if treatment starts in 2012 and anticipatory effects are reasonably only possible 2 years before, this units’ “group” should be labelled as 2010 in the data.

The imputation-based estimators require an additional assumption that the parametric model of \(Y(0) = \mu_i + \eta_t + \varepsilon_{it}\) is correctly specified. This is because in the first stage, you have to accurately impute \(Y(0)\) when residualizing \(Y\) which relies on the correct specification of \(Y(0)\). The 2x2 aggregation models does not impute \(Y(0)\) and hence only relies on a parallel trends assumption. The last column highlights that did allows for uniform inference of estimates. This addresses the problem that multiple hypotheses tests are being done by researchers (e.g. checking individually if all post periods significant) by creating standard errors that adjust for multiple testing.

Example usage of event_study

The result of event_study is a tibble in a tidy format that contains point estimates and standard errors for each relative time indicator for each individual estimator. The results of event_study is a dataframe with event-study term, the estimate, standard error, and a column containing a character for which estimator is used. This output dataframe will in turn be passed to plot_event_study for easy comparison. We return to the df_het dataset to see example usage of these functions.

library(did2s)
#> Loading required package: fixest
#> did2s (v1.0.0). For more information on the methodology, visit <https://www.kylebutts.github.io/did2s>
#> 
#> To cite did2s in publications use:
#> 
#>   Butts, Kyle (2021).  did2s: Two-Stage Difference-in-Differences
#>   Following Gardner (2021). R package version 1.0.0.
#> 
#> A BibTeX entry for LaTeX users is
#> 
#>   @Manual{,
#>     title = {did2s: Two-Stage Difference-in-Differences Following Gardner (2021)},
#>     author = {Kyle Butts},
#>     year = {2021},
#>     url = {https://github.com/kylebutts/did2s/},
#>   }
data(df_het, package = "did2s")
out = event_study(
  data = df_het, yname = "dep_var", idname = "unit",
  tname = "year", gname = "g", estimator = "all"
)
#> Note these estimators rely on different underlying assumptions. See Table 2 of `https://arxiv.org/abs/2109.05913` for an overview.
#> Estimating TWFE Model
#> Estimating using Gardner (2021)
#> Estimating using Callaway and Sant'Anna (2020)
#> Estimating using Sun and Abraham (2020)
#> Estimating using Borusyak, Jaravel, Spiess (2021)
#> Estimating using Roth and Sant'Anna (2021)

head(out)
#>    estimator  term   estimate  std.error
#>       <char> <num>      <num>      <num>
#> 1:      TWFE   -20 0.04097725 0.07167704
#> 2:      TWFE   -19 0.13665695 0.07147683
#> 3:      TWFE   -18 0.14015820 0.07245520
#> 4:      TWFE   -17 0.15793252 0.07431871
#> 5:      TWFE   -16 0.09910002 0.07379570
#> 6:      TWFE   -15 0.20561127 0.07116478
plot_event_study(out, horizon = c(-5,10))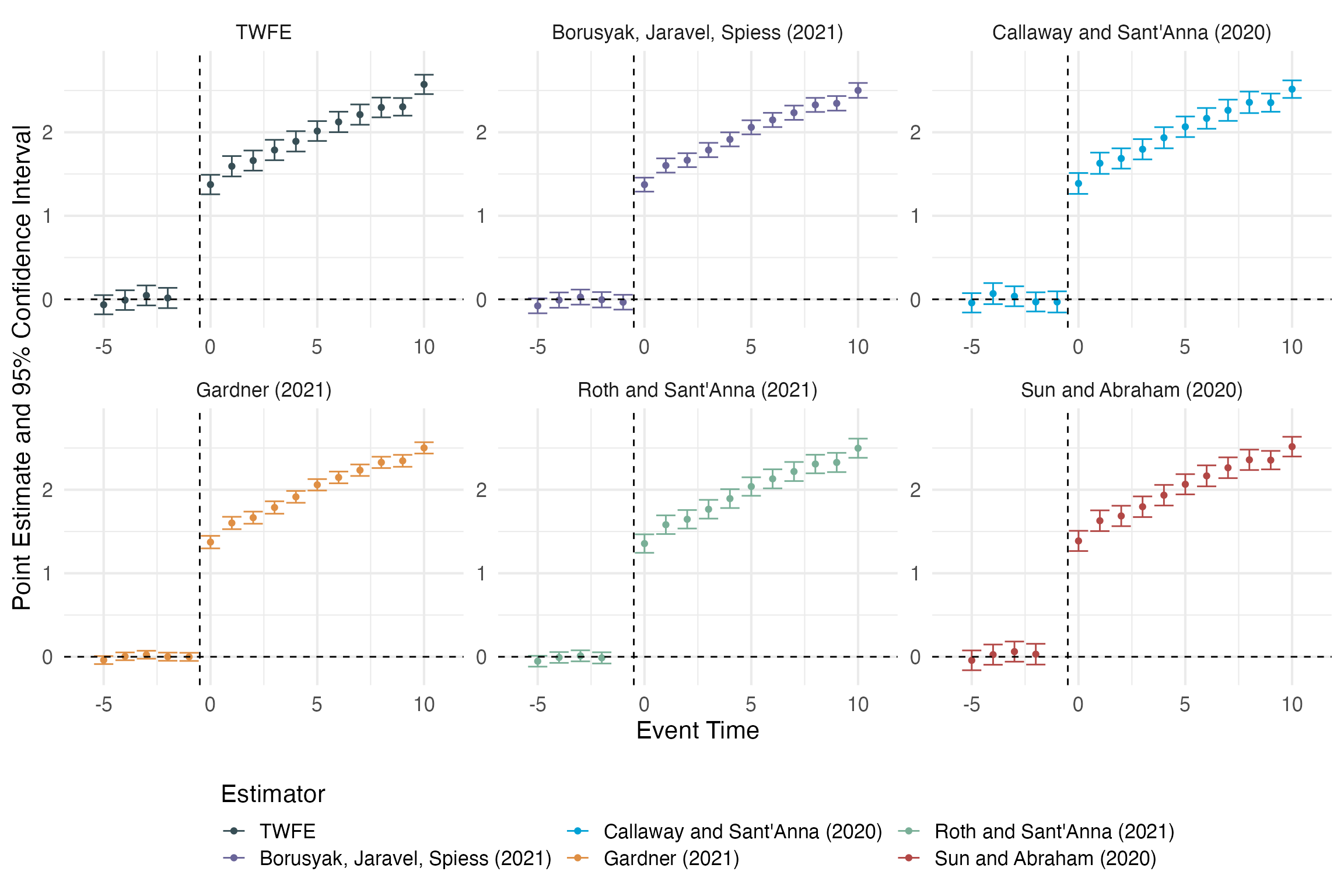
Event-study Estimators

Event-study Estimators